Hard Algebra Questions & Practice Challenge

Ready for a Challenge? Try These Advanced Algebra Problems

Think you’ve mastered the basics? It’s time to level up.

Algebra is the gatekeeper for almost every major college entrance exam and specialized trades test in Canada and the US. But basic equations aren’t enough to guarantee a top score. You need to be comfortable with the “curveballs”—the complex radicals, tricky non-linear graphs, and multi-step inequalities that trip up even the smartest students.

Below, we’ve curated 5 Hard Algebra Questions designed to test your limits. These aren’t just drill questions; they are strategic problems that mirror the toughest sections of the SAT, ACT, and advanced placement exams.

Stuck on a problem? Don’t worry. We have detailed step-by-step solutions below. And if you’re serious about crushing your upcoming exam, check out our Hard Algebra Workbook. It’s packed with hundreds of practice questions, time-saving strategies, and the confidence-boosting drills you need to turn “hard” math into “easy” marks.

• Stop Guessing: Learn the specific steps to dismantle complex problems so you never have to rely on luck.
• Speed Up Your Solving: Master the shortcuts for radicals and exponents that can save you 2-3 minutes per question.
• See the Trap Before You Fall: Identify common “distractor” answers that test makers use to fool unprepared students.
• Build “Math Stamina”: Train your brain to handle difficult, multi-step problems without getting fatigued during the real exam.
• Immediate Feedback: Get detailed, logic-based explanations for every single answer—not just “A” or “B”.

 

Hard Algebra Workbook (PDF Download)   —   Hard Algebra Online Course

1. Simplify expressions with radicals and rational exponents using properties of exponents

A = 2^{2a – 2} and B = 5^{3 – 2a} are given. Find the value of 40^{4a – 2} in terms of A and B.

A) 2 ^. 10^{4 .} (A⁴ / B²)

B) 4 ^. 10^{4 .} (A⁶ / B²)

C) 4 ^. 10^{8 .} (A⁶ / B²)

D) 1.6 ^. 10^{5 .} (A⁶ / B²)

 

2. Analyze rates and proportional relationships and use them to solve real-world mathematical problems

A wall clock shows the time as a quarter past three. After minimum how many minutes will the angle between hour and minute hands be 64⁰?

A) 13

B) 25

C) 37

D) 45

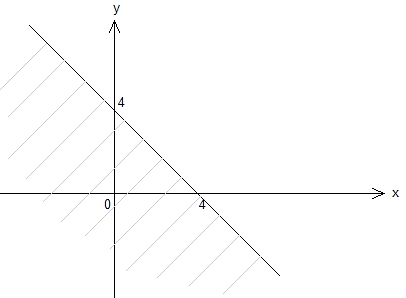
3. Represent and solve nonlinear equations and inequalities graphically

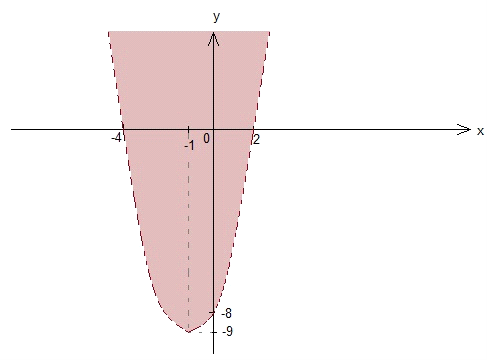
Find the equation of the graph below:

 

A) x² + 2x – 8 > 0

B) 2x + 8y ³ 0

C) x² + 2x – 8 < 0

D) 2x – 8y < 0

 

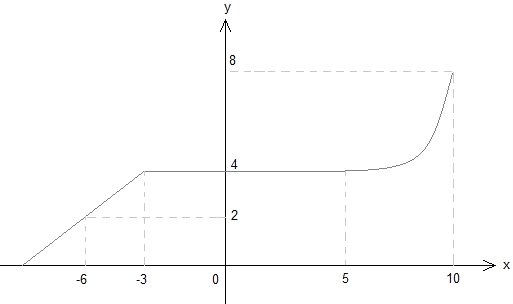
4. Graphs of functions

According to the graph above; find the value of (f(- 3) + f(5) + f(10)) / f^-1(8).

 

A) 1

B) 1.2

C) 1.6

D) 2

 

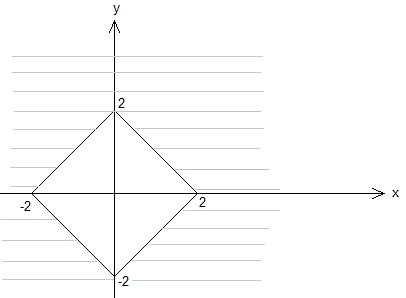
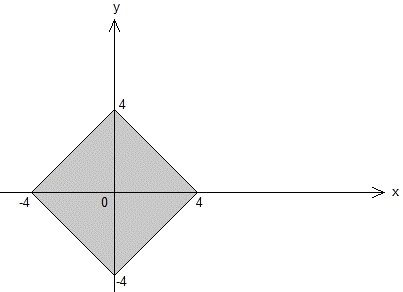
5. Which of the following is the graph of |x| + |y| =< 4?

 

A)

B)

C)

 

D)

1. B

First, we need to be able to write 40 in terms of 2 and 5. By factorisation, we have:

40 = 2^{3 .} 5

So; 40^{4a – 2} = (2^{3 .} 5)^{4a – 2} = 2^{12a .} 2^{-6 .} 5^{4a .} 5^-2

Now, let us write 2^12a and 5^4a in terms of A and B, respectively:

A = 2^{2a – 2} ® 2^2a = 2^{2 .} A ® 2^12a = (2^{2 .} A)⁶ ® 2^12a = 2^{12 .} A⁶

B = 5^{3 – 2a} ® 5^-2a = 5^{-3 .} B ® 5^2a = 5³ / B ® 5^4a = (5³ / B)² ® 5^4a = 5⁶ / B²

Then;

40^{4a – 2} = 2^{12a .} 2^{-6 .} 5^{4a .} 5^-2 = 2^{12 .} A^{6 .} 2^{-6 .} (5⁶ / B²) ^. 5^-2

= (A⁶ / B²) ^. 2^{6 .} 5⁴

= (A⁶ / B²) ^. 2^{4 .} 2^{2 .} 5⁴

= (A⁶ / B²) ^. 10^{4 .} 2²

= 4 ^. 10^{4 .} (A⁶ / B²)

Don’t Solve for the Variable!The most common mistake students make on questions like this is trying to solve for a. Don’t do it! It is a “time trap” designed to waste your valuable exam minutes. Instead of finding the value of a, focus entirely on matching the bases.Notice that your main number is 40, but your “clue” variables (A and B) are defined using bases 2 and 5. That is your roadmap. Your first move must always be Prime Factorization: break the 40 down into 2³ X 5. Once the bases match, this becomes a simple substitution game.

Watch out for: The Distributive Property of Exponents. When you apply the power (4a – 2) to the factors of 40, make sure you apply it to every factor inside the parenthesis.
Many students forget this step and end up with the wrong coefficient!

 

2. A

The whole clock is 360⁰.

Every minute, the minute hand moves 360/60 = 6⁰ and the hour hand moves 360/(60 ^. 12) = 0.5⁰ = 1/2⁰

At 3:15, the minute hand shows directly “3” and the hour hand is 15 ^. 0.5 = 15/2⁰ past it. We expect that the minute hand will get closer and pass the hour hand and then the angle between them will get larger. We are asked to find the time when the angle within the hands is 64⁰. We just need to set a simple equation and solve for x that is the minimum amount of minutes passing:

After x minutes, the minute hand will move 6x angles; the hour hand will move x/2 angles. The minute hand will move 15/2⁰ initially that is the angle between the hands at 3:15; then it will pass the hour hand by 64⁰. So;

6x = 15/2 + x/2 + 64

(11/2)x = 15/2 + 128/2

(11/2)x = 143/2

11x = 143 ® x = 13

After 13 minutes; at 3:28, the angle between hour and minute hands be 64⁰.

Don’t freeze the hour hand! The #1 mistake students make on clock problems is assuming the hour hand stays perfectly still at the “3” while the minute hand moves. Remember, for every minute that passes, the hour hand creeps forward by 0.5⁰.

The Pro Shortcut: Instead of calculating the position of both hands separately, think about Relative Speed. The minute hand moves at 6⁰/min and the hour hand at 0.5⁰/min. This means the minute hand is effectively “chasing” the hour hand at a net speed of 5.5⁰ (or 11/2⁰) per minute.If you set up your equation using 11 / 2 x  represents the gap closing speed, you can often skip the messy decimals and solve it much faster.

Always ask yourself: “Is the minute hand catching up (gap closing) or pulling away (gap widening)?” In this problem, it has to catch up to the hour hand first, then pull away to create the 64⁰ angle.

 

3. C

Let us start analyzing the graph:

Step 1: It shows a quadratic characteristics, the roots of the function are x = – 4 and x = 2. Answer choices B and D are eliminated since they are linear functions.

Step 2: The graph is concave up which means that the term x² has positive coefficient. The vertex passes through (- 1, – 9). The inequality does not cover 0 since the line is dashed.

Point (0, 0) is not included in the inequality. By inserting x = 0 and y = 0, we can check whether A is the answer or C:

x² + 2x – 8 > 0

0² + 2 ^. 0 – 8 > 0

-8 > 0 … this is not a correct statement, so this is not the correct inequality.

x² + 2x – 8 < 0

0² + 2 ^. 0 – 8 < 0

-8 < 0 … this is a correct statement. Yet, it is better that we check the other steps:

Step 1: Find the roots of x² + 2x – 8 = 0:

x² + 2x – 8 = (x + 4)(x – 2) = 0

x = – 4 and x = 2. So, step 1 is proven.

Step 2:

x² + 2x – 8 < 0 … the coefficient of term x² is 1, so the arms of the graph is concave up. The vertex (- 1, – 9) should satisfy x² + 2x – 8 = 0:

(- 1)² + 2(- 1) – 8 = – 9

1 – 2 – 8 = – 9

– 9 = – 9 … The  vertex is correct.

The inequality does not cover 0 since the line is dashed: x² + 2x – 8 < 0. Step 2 is proven.

Strategy Tip: The “Test Point” Zero Hack

Don’t do more algebra than you have to. When you see a graph with a shaded region, your instinct might be to calculate the roots and vertex immediately.

Pause! The fastest way to crack these problems is the Process of Elimination combined with the “Test Point” method.

Check the Shape: Eliminate the linear options (straight lines) immediately. You are looking for a parabola (x²), so cross out B and D instantly.
The Zero Hack: Instead of factoring, pick the easiest point on the grid: (0,0). Look at the graph—is (0,0) inside the shaded area or outside?

If it’s outside (like in this graph), plugging x = 0 and y = 0 into the correct equation must produce a FALSE statement (e.g., -8 > 0 is false).
If it were inside, the equation would produce a TRUE statement.

The Common Trap: Watch out for the Dashed Line vs. Solid Line. A dashed line means the boundary is not included (strictly < or >). A solid line includes the boundary < or >).
Test makers love to give you the correct equation but the wrong inequality symbol—don’t let them fool you!

 

4.  C

Examining the graph, we see that f(- 3) = f(5) = 4; f(10) = 8

f(x) = y ® f^-1(y) = x

So; since f(10) = 8, f^-1(8) = 10

(f(- 3) + f(5) + f(10)) / f^-1(8) = (4 + 4 + 8) / 10 = 1.6

 

 

 

 

Strategy Tip: The “Inverse” vs. “Reciprocal” Trap

Don’t let the notation fool you. The most fatal mistake on this question is thinking that F ^-1(8) means 1 / F (8)} (the reciprocal).

It does not. In function notation, that little -1 is a command to “Swap Your Axis.

“Normal Function F (x): You look at the X-axis to find the Y-value.

Inverse Function F ^-1(y): You look at the Y-axis to find the X-value.

When you see F ^-1(8), translate it into a question: “At what X-value is the height of the graph exactly 8?”

If you trace from y = 8 back to the line, you drop down to x = 10. If you treat it as an exponent, you will get the math wrong every time. Read the graph backwards!

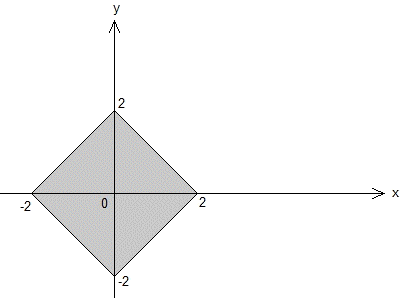
5. D 

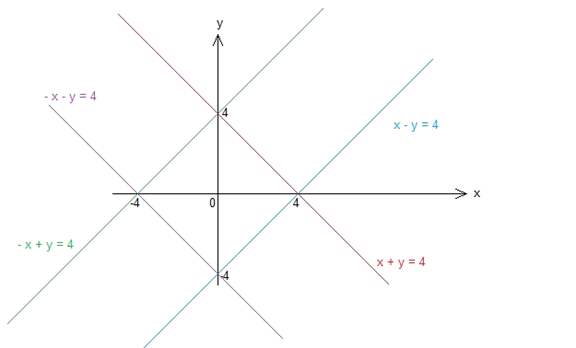
Since this is an absolute value problem, we need to consider negative and positive cases for both x and y:

Let us leave the inequality to the last step and solve |x| + |y| = 4 first:

If x < 0 and y < 0: – x – y = 4

If x < 0 and y > 0: – x + y = 4

If x > 0 and y < 0: x – y = 4

If x > 0 and y > 0: x + y = 4

We obtain four lines. The combination of these four give us the graph of |x| + |y| = 4:

 

Since they are extracted from the same equation; the graph of |x| + |y| = 4 is the rhombus surrounded by

x: [- 4, 4] and y: [- 4, 4].

The function to be drawn the graph of is |x| + |y| £ 4. Checking if origin (0, 0) is within this inequality or not leads us to find the region to be shaded; inside or outside the rhombus:

0 + 0 £ 4 is a correct statement. Therefore, inside region of the rhombus should be shaded.

 

Strategy Tip: The “Diamond” Shortcut

Stop! Put the calculator down. If you try to graph all four linear equations (x + y = 4, -x + y = 4, etc.) separately, you will run out of time.

You need to recognize this specific pattern immediately.

The equation |x| + |y| = k always produces a square tilted on its side (a diamond/rhombus) centered at the origin.
The corners of the diamond are simply the value k on every axis: (4, 0), (-4, 0), (0, 4), and (0,-4).
The Shading Rule: < (Less than): The answer is trapped inside the diamond (closer to the origin).  > (Greater than):
The answer is exploded outside the diamond.
Check your gut: Does (0, 0) work? |0| + |0| < 4. Yes, 0 is less than 4.
So, shade the center. Done. Move to the next question!