Basic Geometry Practice Questions with Full Answer Key – Area, Perimeter, Volume & Angles

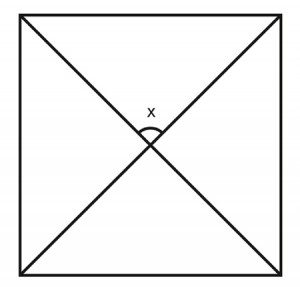
1. What is measurement of the indicated angle assuming the figure is a square?

a. 45^o
b. 90^o
c. 60^o
d. 30^o

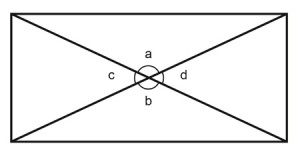
2. What is the sum of all the angles in the rectangle above?

a. 180^o
b. 360^o
c. 90^o
d. 120^o

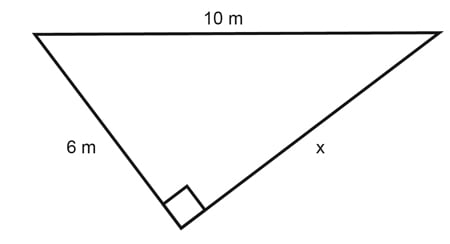
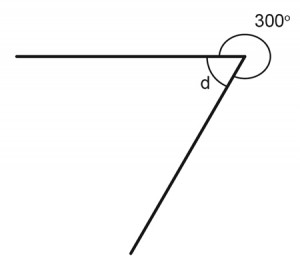
3. What is the measurement of the indicated angle?

a. 45^o
b. 90^o
c. 60^o
d. 50^o

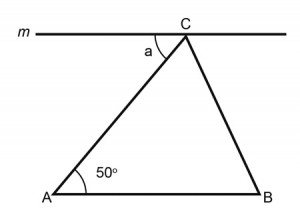
4. If the line m is parallel to the side AB of ?ABC, what is angle a?

a. 130^o
b. 25^o
c. 65^o
d. 50^o

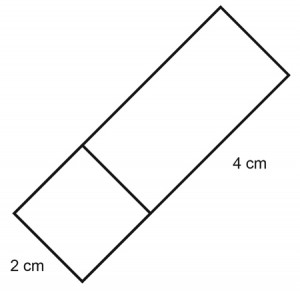
5. What is perimeter of the above shape?

a. 12 cm
b. 16 cm
c. 6 cm
d. 20 cm

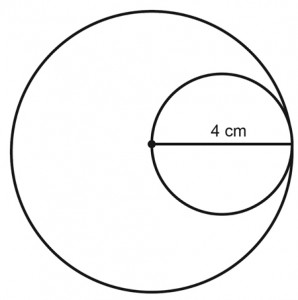
6. What is (area of large circle) – (area of small circle) in the figure above?

a. 8 п cm²
b. 10 п cm²
c. 12 п cm²
d. 16 п cm²

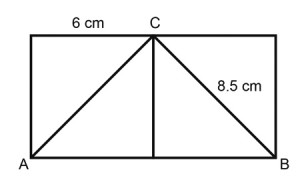
7. What is perimeter of ?ABC in the above shape?

1. 25.5 cm
2. 27 cm
3. 30 cm
4. 29 cm

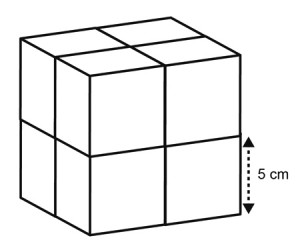
8. What is the volume of the figure above?

a. 125 cm³
b. 875 cm³
c. 1000 cm³
d. 500 cm³

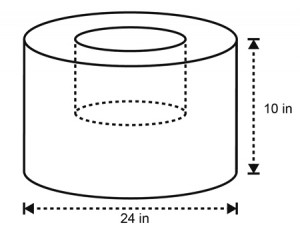
9. What is the volume of the above solid made by a hollow cylinder with half in size of the larger cylinder?

a. 1440 п in³
b. 1260 п in³
c. 1040 п in³
d. 960 п in³

1. B
The diagonals of a square intersect perpendicularly with each other so each angle measures 90^o
x =90^o

2. B
a+b+c+d = ?
The sum of angles around a point is 360^o   a+b+c+d = 360^o

3. C
The sum of angles around a point is 360^o
d+300 = 360^o
d = 60^o

4. D
Two parallel lines(m & side AB) intersected by side AC
a= 50^o (interior angles)

5. B
The square with 2 cm side common to the rectangle apart from 4cm side
Perimeter = 2+2+2+4+2+4 = 16 cm

6. C
In the figure, we are given a large circle and a small circle inside it;
with the diameter equal to the radius of the large one. The diameter of the
small circle is 4 cm. This means that its radius is 2 cm. Since the diameter
of the small circle is the radius of the large circle, the radius of the large
circle is 4 cm. The area of a circle is calculated by: пr² where r is the
radius.  Area of the small circle: п(2)² = 4п Area of the large circle: п(4)²2 = 16п

The difference area is found by:
Area of the large circle – Area of the small circle = 16п – 4п = 12п

7. D
Perimeter of a shape with two squares and triangle ABC.
Perimeter = 8.5+8.5+6+6
Perimeter = 29 cm.

8. C
Large cube is made up of 8 smaller cubes of 5 cm sides.
Volume = Volume of small cube x 8
Volume = (5 x 5 x 5) x 8, 125 x 8
Volume = 1000cm³

9. B
Volume= Volume of large cylinder – Volume of small cylinder
(Volume of cylinder = area of  base x height)
We know the small cylinder is 1/2 the size of the large cylinder
So, Volume of the small cylinder
= Large Cylinder (п 12²x 10) – Small Cylinder(п 6²x 5)
= 1440п – 180п
Volume of small cylinder = 1260п in³

See also our tutorial on Complex Shapes

Common geometry questions on on standardized tests :

• Solve for the missing angle or side
• Finding the area or perimeter of different shapes (e.g. triangles, rectangles, circles)
• Problems using the Pythagorean Theorem
• Calculate properties of geometric shapes such as angles, right angles or parallel sides
• Calculating volume or surface area of complex shapes for example spheres, cylinders or cones
• Solve geometric transformations such as rotation, translation or reflections

1. Not clearly labeling or identifying the given and unknown information in a problem
2. Not understanding the properties and definitions of basic geometric figures (e.g. line, angle, triangle, etc.)
3. Incorrectly using basic formulas (e.g. area of a triangle, Pythagorean theorem)
4. Incorrectly interpreting geometric diagrams
5. Not understanding the relationship between parallel lines and transversals
6. Not understanding the relationship between angles and their degree measures
7. Not understanding the relationship between perimeter and area