Geometric Transformations

If we want to move a geometric shape, or change its direction or size, we would use one of the following geometric transformations:

1) Dilation
2) Translation
3) Rotation
4) Reflection

Tests that have geometric transformation questions:

ACCUPLACER —  ACT  —  CHSPE  —  College Math  —  Compass  —  CUNY  —  NYSTCE

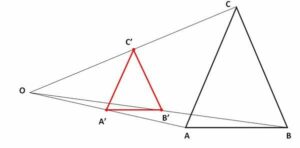
Dilation is transformation where 2D shape is either enlarged or contracted, where the direction of the shape is kept. If we have a triangle ABC that we want to reduce to a new triangle half of its size, we would make an arbitrary point of dilation O and connect it with points A, B and C.

We find the centers of lines OA, OB and OC and mark  them as A’, B’ and C’, respectively. We cut the lines in half because we want the new triangle to be half the size of the original one. These new points make the triangle A’B’C’ which is the one we are looking for.

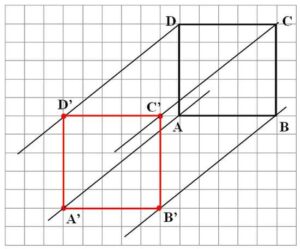
Translation is a transformation we use for moving the 2D shapes, without changing their size or direction. It can be moved using a grid or a coordinate system. If we have a square ABCD in a grid we want to move 6 units to the left  and 5 units down, we move each point of the square and we connect the new points, where we get a new square A’B’C’D’ with exactly same size and direction.

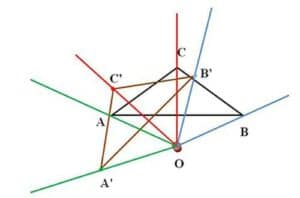
Rotation is a transformation where we only change the direction of a 2D shape, but not the size. We make an arbitrary center of the rotation O, and if we want to rotate a triangle ABC by, for example, 45⁰, then we rotate every point of the triangle by 45⁰, where we have that OA is  equal to OA’, and same goes for OB and OC.

The triangle A’B’C’ is actually triangle ABC rotated by 45⁰.

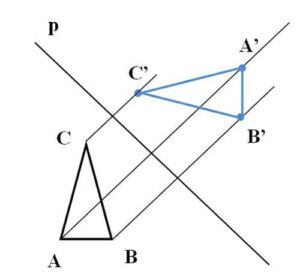
Reflection is a transformation where we make a mirror image of some 2D shape. Reflection changes the direction of the shape, but not its size. We are given a mirror line p which we use to reflect each point of the shape doing this: we make a line through each point of the shape, in this case of the triangle ABC, and these lines should intersect the mirror line p at right angle, we then measure the distance from the intersection and the original point and we find the mirror point using that distance. We connect
mirror points and we get a reflected triangle A’B’C’.

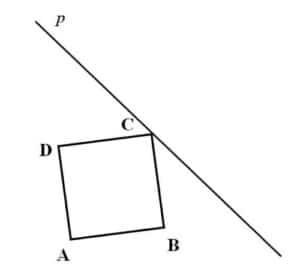
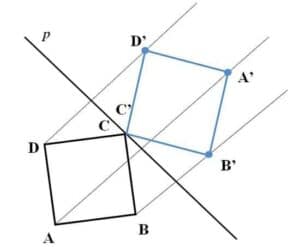
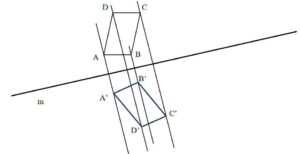
Reflect the square ABCD with the given mirror line p.

Since the point C is already on the mirror line, we don’t have to reflect it. From points A, B and D we draw the lines that intersect with the mirror line at right angle. We measure the distance from the mirror line to the A, B and D and we use those distance to find points A’, B’ and D’, respectively, on the same line on the other side of the mirror line.

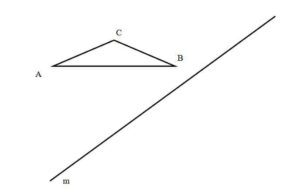
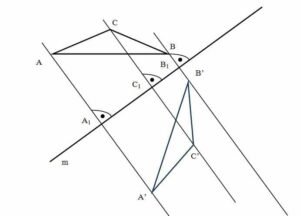
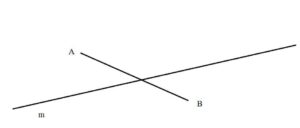
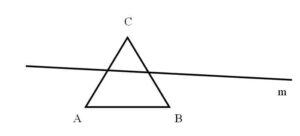
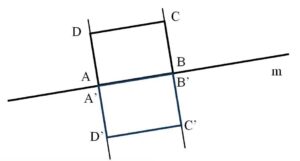
2. Reflect triangle ABC against the mirror line m that are given in the figure below.

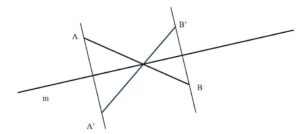
We draw lines from each point of the triangle ABC which will intersect with the mirror line at the right angle. We measure the distance from the triangle’s points to the line m, and we use them to find points A’, B’ and C’. We connect the new points and we get a reflection of the triangle ABC, that is triangle A’B’C’.

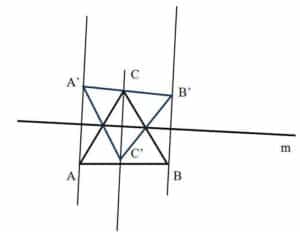
Let’s see a different example: What if we have a geometrical shape that intersects with the mirror line, like line AB?

We reflect points A and B, no matter if they are on the different sides of the mirror line.

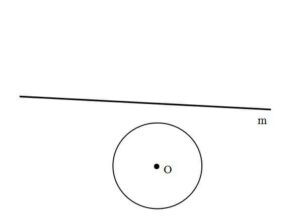
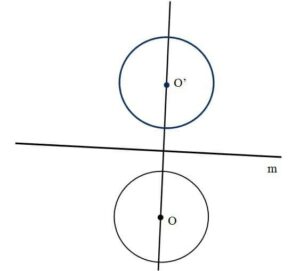
1. Reflect the circle with the center in O with the given mirror line m.

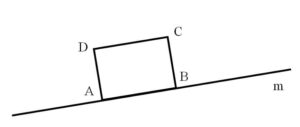
2. Reflect the rectangle ABCD with the given mirror line m in the space below.

3. Reflect the triangle ABC with the given mirror line m in the space below.

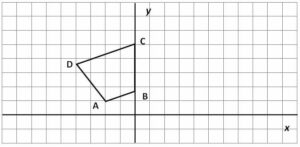
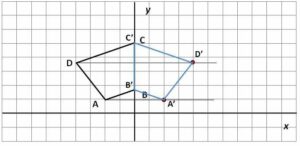
4. Reflect the quadrilateral ABCD in the coordinate plane if the mirror line is y-axis.

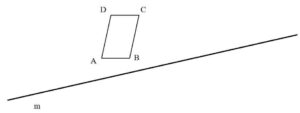
5. Reflect the parallelogram ABCD with the given mirror line m.

1. We reflect the center O against the mirror line m at right  angle and we use a compass to draw the circle with the same radius as the original circle.

2. We reflect points C and D against the mirror line m at the right angle. Since points A and B are already on the mirror line, we can’t reflect them and that’s why A coincides with point A’ , and the same goes for points B and B’.

3. We reflect points A, B and C against the mirror line m at the right angle and we connect the new points A’, B’ and C’. The process is the same even though the points of the triangle are not on the same side of the mirror line.

4. The reflected geometric shapes process is the same in the coordinate plane. Here, our mirror line is y-axis, so we reflect points A and D, and points B and C are already on the mirror line, so we don’t reflect them.

5. We reflect points A, B, C and D against the mirror line m at right angle and we connect the new points A’, B’,C’ and D’.