Inverse Functions Practice Questions

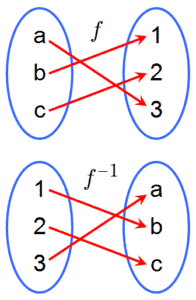
An inverse function (or anti-function) is a function that “reverses” another function: if the function f applied to an input x, and gives a result of y, then the inverse function g, applied to y,  gives the result x, and vice versa, i.e., f(x) = y if and only if g(y) = x

Key Concepts

1. Definitions
2. Function Notation
3. Determine the Inverse Function

1. Definitions

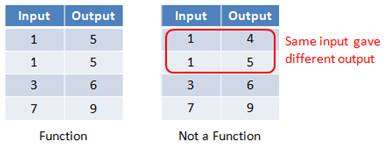
Function – A set of data such that every input (x) has EXACTLY ONE output (y)

Inverse Function – The result of SWITCHING the input (x) with the output (y)

1. Function Notation

A set of data must have exactly one output for each input, though multiple inputs may have the same output.

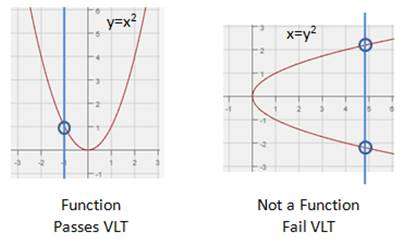
An equation is written in function notation by replacing “y” with “f(x)” (pronounced “f of x”).  Function notation does NOT mean “f times x”!  The equation is a function if its graph passes the Vertical Line Test (VLT).  The VLT states that if any vertical line can be drawn and touches the graph at more than 1 point, the graph is not a function.

1. Determine the Inverse of a Function

To determine the inverse of a function, simply switch the x and y variables.  It is commonly accepted to rewrite the inverse equation in slope-intercept form.  [Note: Sometimes an original equation is a function, but its inverse is not.]  An inverse function is NOT related to the concept of a reciprocal.

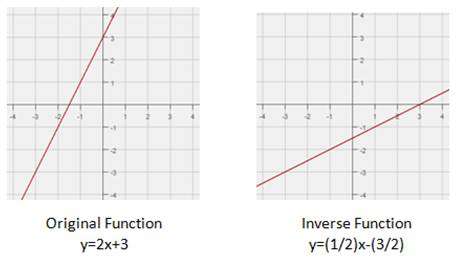
Ex. Determine the inverse of the given equation.

y=2x+3

Solution:
Step 1 – Exchange the x and y variables.
(x)=2(y)+3

Step 2 – Solve for y.
2y=x-3
y=(1/2)x-(3/2)

Note: The graphs of a

function and its inverse (if it exists) are reflections across the line y=x.

1. Find the inverse function of the function f(x) = 3x + 3.

a. (3x – 1) / 3
b. (x + 1) / 3
c. (x – 1) / 3
d. (x – 3) / 3

2. Find the inverse function of the function f(x) = (5x – 2) / 4.

a. (4x – 1) / 5
b. (x + 4) / 5
c. (4x + 2) / 5
d. (4x – 2) / 5

3. Find f ^-1(1/2)  if  f(x) = 1 – x.

a. 1
b. 1/2
c. 1/3
d. 1/4

4. If f(x) = 5x and g(x) = 7 – 2x, find (f – g)^-1 (0).

a. 1
b. 2
c. 3
d. 4

5. If f ^-1 (x) = 2x, find f(x).

a. x
b. 2x
c. x/2
d. x/3

1. D (x-3)/3

f(x) = 3x + 3

f ^-1(f(x)) = x

f ^-1 (3x + 3) = x

3x + 3 = t

3x = t – 3

x = (t – 3) / 3

 f ^-1(t) =  (t – 3) / 3

 f ^-1(x) = (x – 3) / 3

2. C. (4x + 2) / 5

f(x) = (5x – 2) / 4

f ^-1(f(x)) = x

f ^-1((5x – 2) / 4) = x

(5x – 2) / 4 = t

5x – 2 = 4t

5x = 4t + 2

x = (4t + 2) / 5

 f ^-1(t) = (4t + 2) / 5

f ^-1(x) = (4x + 2) / 5

3. B. 1/2

f(x) = 1 – x

f ^-1(1-x) = x

1 – x = t

x = 1 – t

 f ^-1(t) = 1 – t

 f ^-1(x) = 1 – x

 f ^-1(1/2) = 1 – 1/2 = 1/2

4. A. 1

f(x) = 5x

g(x) = 7 – 2x

 f(x) – g(x) = 5x – (7 – 2x) = 5x – 7 + 2x = 7x – 7

(f(x) – g(x))^-1(f(x) – g(x)) = x

(f(x) – g(x))^-1(7x – 7) = x

7x – 7 = t

7x = t + 7

x = (t + 7) / 7

(f(t) – g(t))^-1(t) = (t + 7) / 7

(f(x) – g(x))^-1(x) = (x + 7) / 7

(f(x) – g(x))^-1(0) = (0 + 7)/7 = 1

5. C. x/2

f ^-1(f(x))=x       We treat f(x) as a variable, so instead of 2x we have 2f(x).

2f(x) = x

 f(x) = x/2