Trigonometry Review and Practice Questions

Trigonometry is the branch of mathematics dealing with the relations of the sides and angles of triangles and with the relevant functions of any angles.

College Level Math – Trigonometry questions appear on tests that have College Level Math questions such as the Accuplacer and the Compass.

Review     Practice Questions     Answer Key

Quick Review with Examples

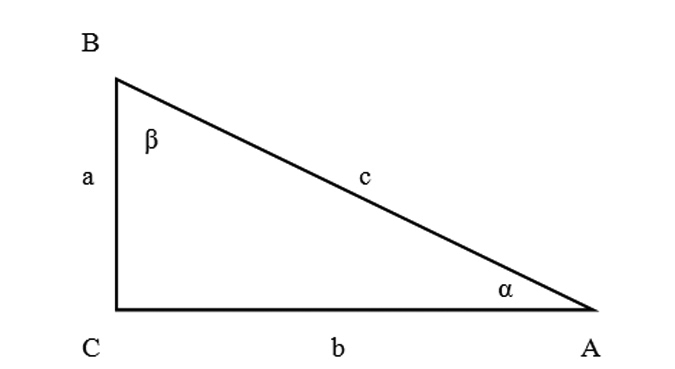
If we are observing a right triangle, where a and b are its legs and c is its hypotenuse, we can use trigonometric functions to make a relationship between angles and sides of the right triangle.

If the right angle of the right triangle ABC is at the point C, then the sine (sin) and the cosine (cos) of the angles α (at the point A) and β (at the point B) can be found like this:

             sinα = a/c         sinβ = b/c

                        cosα = b/c         cosβ = a/c

Notice that sinα and cosβ are the equal, and same goes for sinβ and cosα. So, to find sine of the angle, we divide the side that is opposite of that angle and the hypotenuse. To find cosine of the angle, we divide the side that makes that angle (adjacent side) by the hypotenuse.

There are 2 more important trigonometric functions, tangent and cotangent:

tgα = sinα/cosα = a/b

                        ctgα = cosα/sinα = b/a

For the functions sine and cosine, there is a table with values for some of the angles, which is to be memorized as it is very useful for solving various trigonometric problems. Here is that table:

√

	0⁰	30⁰	45⁰	60⁰	90⁰
sinα	0	1/2	√2/2	√3/2	1
cosα	1	√3/2	√2/2	1/2	0

Let’s see one example:

If a is 9 cm and c is 18 cm, find α.

We can use the sine for this problem:

sinα = a/c = 9/18 = 1/2

We can see from the table that if sinα is 1/2, then angle α is 30⁰.

In addition to degrees we can write angles using π, where π represents 180⁰. For example, angle π/2 means a right angle of 90⁰.

 

 

Practice Questions

 

1. If sides a and b of a right triangle are 8 and 6, respectively, find cosine of α.

a. 1/5
b. 5/3
c. 3/5
d. 2/5

2. Find tangent of a right triangle, if a is 3 and b is 5.

a. 1/4
b. 5/3
c. 4/3
d. 3/4

3. If α=30⁰, find sin30⁰ + cos60⁰.

a. 1/2
b. 2/3
c. 1
d. 3/2

4. Calculate (sin²30⁰ – sin0⁰)/(cos90⁰ – cos60⁰).

A. -1/2
B. 2/3
C. 0
D. 1/2

5. Find cotangent of a right angle.

A. -1
B. 0
C. 1/2
D. -1/2

 

Answer Key 

1. C 3/5

a=8
b=6
a²+b²=c²
8²+6²=c²
64+36= c²
c²=100
c=10
cosα = b/c = 6/10 = 3/5

2. D 3/4
a = 3
c = 5
a2+b2=c2
32 + b² = 5²
b² = 25 – 9
b² = 16
b = 4
tgα = a/b = 3/4

3. C 1
α=30⁰
sin30⁰ + cos60⁰ = 1/2 + 1/2 = 1

4. A. -1/2

(sin²30⁰– sin0⁰) / (cos90⁰ – cos60⁰) = ((1/2)² – 0) / (0 – 1/2) = (1/4) / (-1/2) = -1/2

5. B. 0

α=90⁰
ctg90⁰ = cos90⁰/ sin90⁰ = 0/1 = 0

Written by: Brian Stocker MA, Complete Test Preparation Inc.
Modified: December 18th, 2018 December 18th, 2018

Published: June 20th, 2014