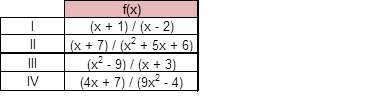Math Functions Practice with Answer Key
Practice Questions:
1. Find g○f if f(x) = 2x + 5 and g(x) = 5x + 2.
A. 5x + 5
B. 10x + 27
C. 10x + 2
D. 25x + 25
E. 4x + 10
2. If f(x) = 1 + x2, find f○f .
A. 1 + x2 + x4
B. 2 + x2 + x4
C. 2 + x2
D. 1 + x4
3. If f(x) = -x, g(x) = 2x + 1 and h(x) = x2, find f○g○h .
A. x2 – 1
B. 2x2 – 1
C. x2 – 2
D. x2 + 1
E. x2 + 2
4. Which of the following functions have the largest domain?
A. I
B. II
C. III
D. IV
Answer Key
1. B. 10x + 27
f(x) = 2x + 5
g(x) = 5x + 2.
g○f = g(f(x)) = g(2x + 5) = 5(2x + 5) + 2 = 10x + 25 + 2 = 10x + 27
2. D. 2+2×2+x4
f(x)=1+x2
f○f=f(f(x))=f(1+x2)=1+(1+x2)2=1+1+2×2+x4=2+2×2+x4
3. B. -2x2 – 1
f(x) = -x
g(x) = 2x + 1
h(x) = x2
f○g○h = f(g(h(x))) = f(g(x2)) = f(2x2 + 1) = -(2x2 + 1) = -2x2 – 1
3. C
Without any restrictions, the domain of a function is (-∞, +∞). The restrictions are found by checking the denominator of the function. If there are any values that make the denominator zero; since division by zero is undefined, these x values should be eliminated from the domain:
f(x) = (x + 1) / (x – 2) : Notice that the denominator is x – 2 and x = 2 value makes it zero, so makes the function undefined. The domain of this function is (-∞, +∞) – {2}.
f(x) = (x + 7) / (x2 + 5x + 6) : Notice that the denominator is x2 + 5x + 6 which can be factorised as
(x + 2)(x + 3). Then, x = – 2 and x = – 3 values make the denominator zero, so make the function undefined. The domain of this function is (-∞, +∞) – {- 3, – 2}.
f(x) = (x2 – 9) / (x + 3) : Notice that first, it is possible to simplify the function:
f(x) = (x2 – 9) / (x + 3) = (x + 3)(x – 3) / (x + 3) = x – 3. Then, the denominator has vanished; the domain of this function is (-∞, +∞).
f(x) = (4x + 7) / (9x2 – 4) : Notice that the denominator is 9x2 – 4 which can be factorised as
(3x – 2)(3x + 2). It is not possible to simplify. Then, x = 2/3 and x = – 2/3 values make the denominator zero, so make the function undefined. The domain of this function is (-∞, +∞) – {- 2/3, 2/3}.
Function (x2 – 9) / (x + 3) has the largest domain.
The correct answer is (C).
