Basic Geometry – Area of Complex Shapes
Area and Perimeter of Complex Shapes
Area and Perimeter of Complex ShapesComplex figures can be divided into several smaller shapes where the perimeter or area formula is known, then added.
[wptouch target=”mobile”]
Basic Math Practice
Fractions, Percent
and Decimals
Area and Perimeter of Complex Shapes
Math Test Prep
[/wptouch]
Example – Composite 2-D shapes
To determine the area of any composite figure, simply ADD the areas of each component basic figure. Be sure to write your final answer with square units.
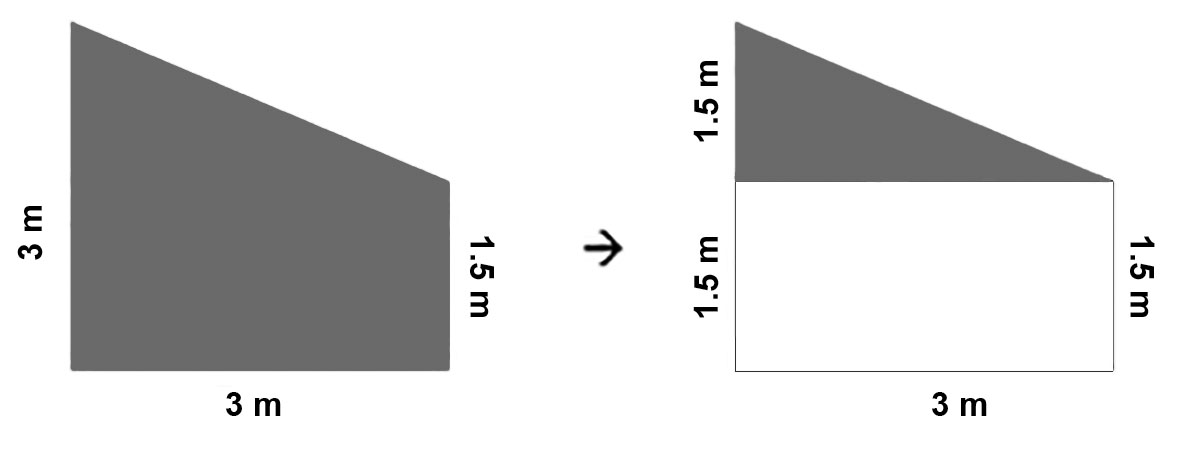
Determine the area of the given shape.
The original shape can be redrawn as a rectangle and a triangle. Rectangles have opposite sides that are congruent (exactly the same).
Area Composite = Area Triangle + Area Rectangle
Area Triangle = (1/2)(Base)(Height) = (1/2)(3m)(1.5m) = 2.25 m2
Area Rectangle = (Base)(Height) = (3m)(1.5m) = 4.5 m2
Area Composite = (2.25m2) + (4.5m2) = 6.75 m2
Determine the Surface Area of a Composite 3-D Solid
To determine the surface area of any composite solid, simply add the surface areas of each component basic solid. You must also subtract the area of any internal face. Be sure to write your final answer with square units.
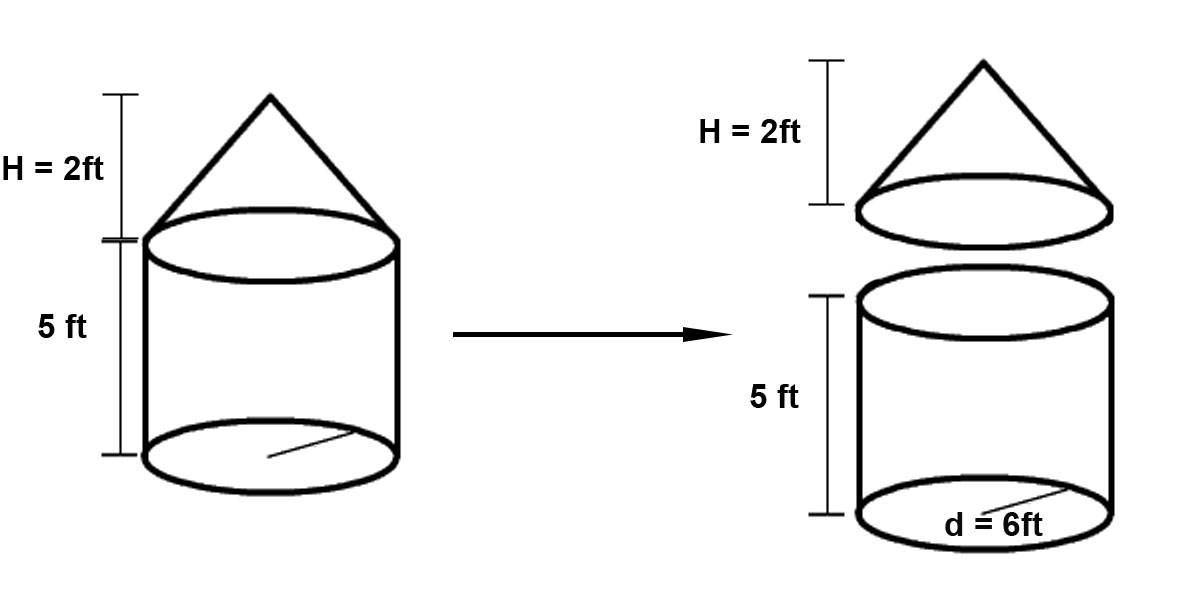
Ex. Determine the surface area of the given shape. Leave the final answer in terms of pi.
The original shape can be redrawn as a cylinder and a cone. We will have to subtract the area of the circle where the figures meet from each surface area equation because they are “inside” the solid.
SurfaceArea Composite = S.Area Cone + S.Area Cylinder
S.Area Cone = (Base Area)+(1/2)(Perimeter)(Height) = (1/2)(dπ)(h) = (1/2)(6π)(2) = 6π ft2
S.Area Cylinder = 2(Base Area)+(Perimeter)(Height) = (πr2)+(dπ)(h) = (π32)+(6π)(5) = 39π ft2
S.Area Composite = (6π ft2) + (39π ft2) = 45π ft2
Written by: Brian Stocker MA, Complete Test Preparation Inc.
Modified: December 13th, 2018
Published: October 9th, 2017
You may also like
Listening Comprehension Practice – Solving a Problem
After you take a Practice Test
