Pythagorean Geometry – Tutorial and Practice Questions
- Posted by Brian Stocker
- Date February 13, 2019
- Comments 1 comment
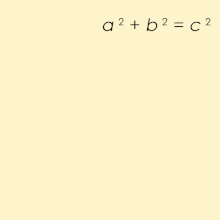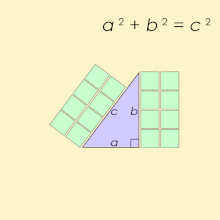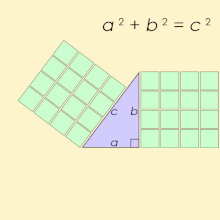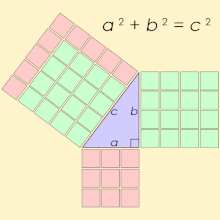
A Pythagorean triple consists of three positive integers a, b, and c, such that a2 + b2 = c2. Such a triple is commonly written (a, b, c), and a well-known example is (3, 4, 5). If (a, b, c) is a Pythagorean triple, then so is (ka, kb, kc) for any positive integer k. A primitive Pythagorean triple is one in which a, b and c are coprime (that is, they have no common divisor larger than 1). A triangle whose sides form a Pythagorean triple is called a Pythagorean triangle, and is necessarily a right triangle.
Questions on basic geometry and Pythagorean geometry are on most high school tests
Pythagorus – A Quick Review and Tutorial
If we have a right triangle ABC, where its sides (legs) are a and b and c is a hypotenuse (the side opposite the right angle), then we can establish a relationship between these sides using the following formula:
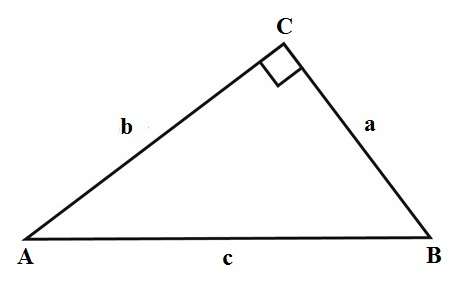
This formula is proven in the Pythagorean Theorem. There are many proofs of this theorem, but we’ll look at just one geometrical proof:
If we draw squares on the right triangle’s sides, then the area of the square upon the hypotenuse is equal to the sum of the areas of the squares that are upon other two sides of the triangle. Since the areas of these squares are a2, b2 and c2, that is how we got the formula above.
One of the famous right triangles is one with sides 3, 4 and 5. And we can see here that:
32 + 42 = 52
9 + 16 = 25
25 = 25
Example:
We write the information we have about triangle ABC and we draw a picture of it for better understanding of the relation between
its elements:
P = 18 cm
a – b = 3 cm
h=?
We use the formula for the perimeter of the isosceles triangle, since that is what is given to us:
P = a + 2b = 18 cm
Notice that we have 2 equations with 2 variables, so we can solve it as a system of equations:
a + 2b = 18
a – b = 3 / multiply by 2
a + 2b = 18
2a – 2b = 6
a + 2b + 2a – 2b = 18 + 6
3a = 24
a = 24:3 = 8 cm
Now we go back to find b:
a – b = 3
8 – b = 3
b = 8 – 3
b = 5cm
Another Example
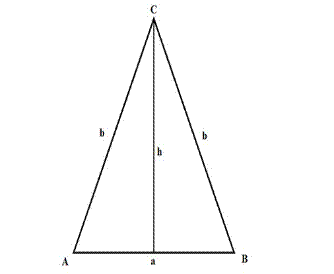
We write the information we have about triangle ABC and we draw a picture of it for better understanding of the relation between
its elements:
P = 18 cm
a – b = 3 cm
h = ?
We use the formula for the perimeter of the
isosceles triangle, since that is what is given to us:
P = a + 2b = 18 cm
Notice that we have 2 equations with 2 variables, so we can solve it as a system of equations:
a + 2b = 18
a – b = 3 / multiply by 2
a + 2b = 18
2a – 2b = 6
a + 2b + 2a – 2b = 18 + 6
3a = 24
a = 24:3 = 8 cm
Now we go back to find b:
a – b = 3
8 – b = 3
b = 8 – 3
b = 5cm
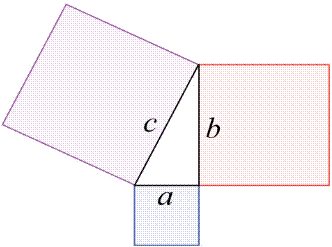
Using Pythagorean Theorem, we can find the height using a and b, because the height falls on the side a at the right angle. Notice that height cuts side a exactly in half, and that’s why we use in the formula a/2. In this case, b is our hypotenuse, so we have:
Pythagorean Geometry – Practice Questions
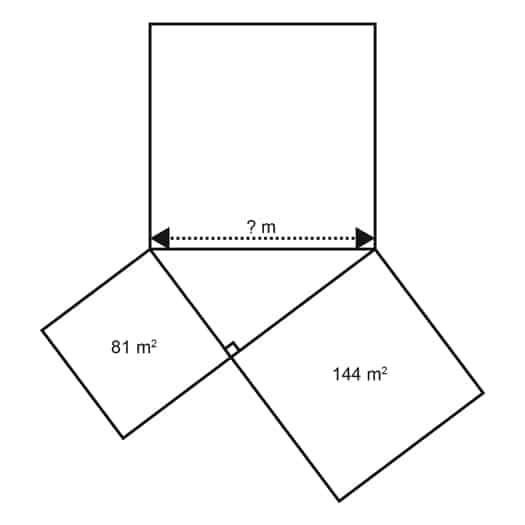
1. What is the length of each side of the indicated square above?
a. 10
b. 15
c. 20
d. 5
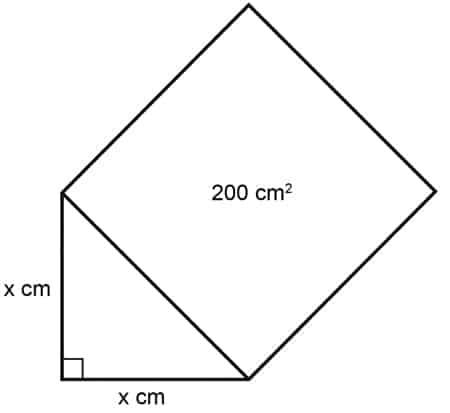
2. What is the length of the sides in the triangle above?
a. 10
b. 20
c. 100
d. 40
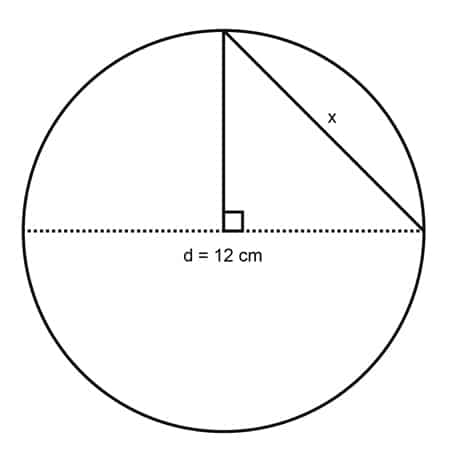
3. For the given diameter, what is the square of the indicated measurement?
a. 6
b. 72
c. 36
d. 64
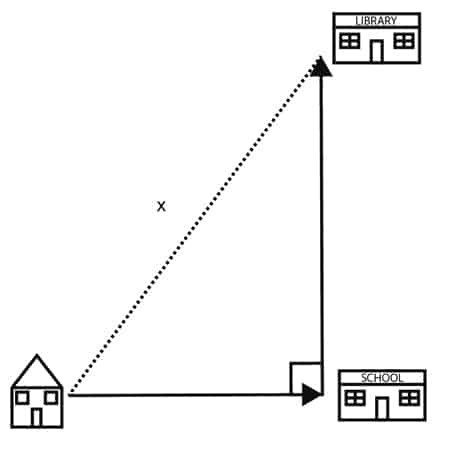
4. Every day starting from his home Peter travels due east 3 kilometers to the school. After school he travels due north 4 kilometers to the library. What is the distance between Peter’s home and the library?
a. 15 km
b. 10 km
c. 5 km
d. 12 ½ km
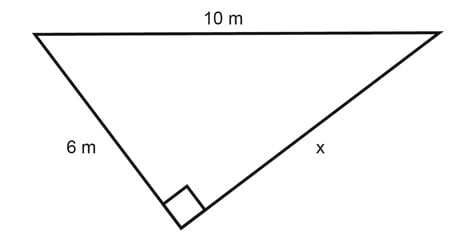
5. What is the length of the missing side in the triangle above?
a. 6
b. 4
c. 8
d. 5
Answer Key

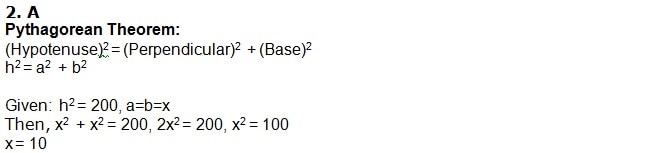

4. C
Pythagorean Theorem:
(Hypotenuse)2 = (Perpendicular)2 + (Base)2
h2 = a2 + b2
Given: 32 + 42 = h2
h2 = 9 + 16
h = √25
h = 5

Most Popular Geometry Questions
Common geometry questions on on standardized tests :
- Solve for the missing angle or side
- Finding the area or perimeter of different shapes (e.g. triangles, rectangles, circles)
- Problems using the Pythagorean Theorem
- Calculate properties of geometric shapes such as angles, right angles or parallel sides
- Calculating volume or surface area of complex shapes for example spheres, cylinders or cones
- Solve geometric transformations such as rotation, translation or reflections
Most Common Geometry Mistakes on a Test
- Not clearly labeling or identifying the given and unknown information in a problem
- Not understanding the properties and definitions of basic geometric figures (e.g. line, angle, triangle, etc.)
- Incorrectly using basic formulas (e.g. area of a triangle, Pythagorean theorem)
- Incorrectly interpreting geometric diagrams
- Not understanding the relationship between parallel lines and transversals
- Not understanding the relationship between angles and their degree measures
- Not understanding the relationship between perimeter and area
Date Published: Wednesday, February 13th, 2019
Date Modified: Wednesday, June 14th, 2023
Got a Question? Email me anytime - Brian@test-preparation.ca
You may also like
CELPIP Writing Prompts
The CELPIP writing evaluates your ability to communicate effectively in written English different tasks. Here are some sample CELPIP Writing prompts for writing an exmail. You are given a prompt and a scenario. Your email may be formal or informal, …
CCAT Vocabulary Practice – Grades 4 – 5
1. What is the definition of the word ‘polygon’? a. A curved line b. A straight line c. A closed plane figure with straight sides d. A round shape 2. Which term means to ‘depict or show something’? a. Represent …
Vocabulary Practice for Grades 4 & 5
1. What is a “polygon”? A) A three-dimensional shape B) A figure with multiple angles and sides C) A type of line segment D) A type of angle 2. What does the word “represent” mean? A) To take away something …

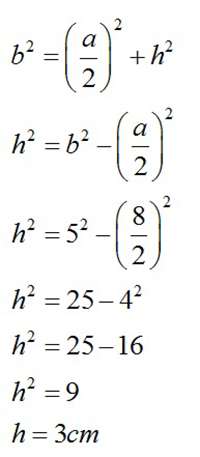
1 Comment
The Pythagorean formula is the SUM of a and b – a2 + b2 = c2