Hard Algebra Questions

Advanced Algebra Practice

1. Simplify expressions with radicals and rational exponents using properties of exponents

A = 2^{2a – 2} and B = 5^{3 – 2a} are given. Find the value of 40^{4a – 2} in terms of A and B.

A) 2 ^. 10^{4 .} (A⁴ / B²)

B) 4 ^. 10^{4 .} (A⁶ / B²)

C) 4 ^. 10^{8 .} (A⁶ / B²)

D) 1.6 ^. 10^{5 .} (A⁶ / B²)

 

2. Analyze rates and proportional relationships and use them to solve real-world mathematical problems

A wall clock shows the time as a quarter past three. After minimum how many minutes will the angle between hour and minute hands be 64⁰?

A) 13

B) 25

C) 37

D) 45

3. Represent and solve nonlinear equations and inequalities graphically

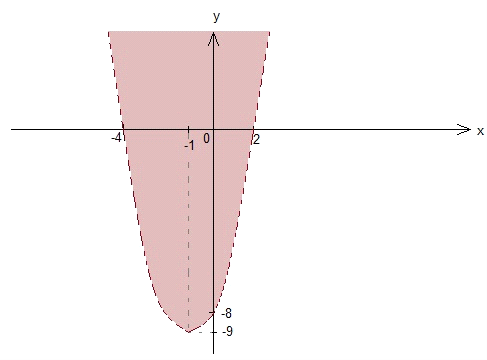
Find the equation of the graph below:

 

A) x² + 2x – 8 > 0

B) 2x + 8y ³ 0

C) x² + 2x – 8 < 0

D) 2x – 8y < 0

 

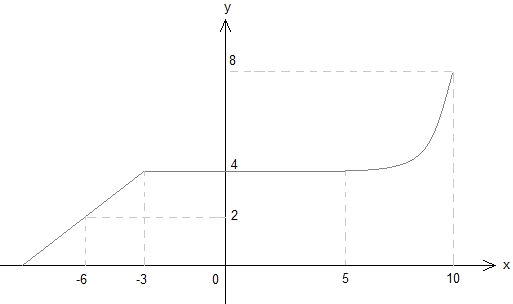
4. Graphs of functions

According to the graph above; find the value of (f(- 3) + f(5) + f(10)) / f^-1(8).

 

A) 1

B) 1.2

C) 1.6

D) 2

 

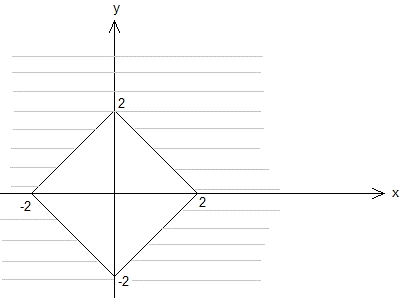
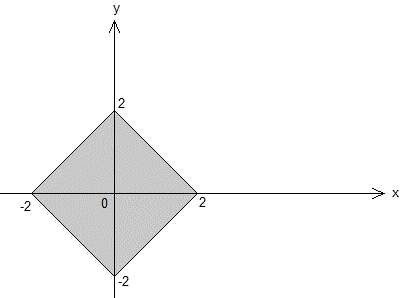
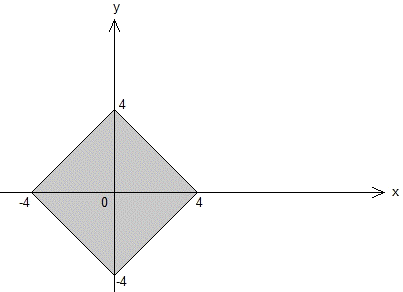
5. Which of the following is the graph of |x| + |y| =< 4?

 

A)

B)

C)

 

D)

1. B

First, we need to be able to write 40 in terms of 2 and 5. By factorisation, we have:

40 = 2^{3 .} 5

So; 40^{4a – 2} = (2^{3 .} 5)^{4a – 2} = 2^{12a .} 2^{-6 .} 5^{4a .} 5^-2

Now, let us write 2^12a and 5^4a in terms of A and B, respectively:

A = 2^{2a – 2} ® 2^2a = 2^{2 .} A ® 2^12a = (2^{2 .} A)⁶ ® 2^12a = 2^{12 .} A⁶

B = 5^{3 – 2a} ® 5^-2a = 5^{-3 .} B ® 5^2a = 5³ / B ® 5^4a = (5³ / B)² ® 5^4a = 5⁶ / B²

Then;

40^{4a – 2} = 2^{12a .} 2^{-6 .} 5^{4a .} 5^-2 = 2^{12 .} A^{6 .} 2^{-6 .} (5⁶ / B²) ^. 5^-2

= (A⁶ / B²) ^. 2^{6 .} 5⁴

= (A⁶ / B²) ^. 2^{4 .} 2^{2 .} 5⁴

= (A⁶ / B²) ^. 10^{4 .} 2²

= 4 ^. 10^{4 .} (A⁶ / B²)

 

2. A

The whole clock is 360⁰.

Every minute, the minute hand moves 360/60 = 6⁰ and the hour hand moves 360/(60 ^. 12) = 0.5⁰ = 1/2⁰

At 3:15, the minute hand shows directly “3” and the hour hand is 15 ^. 0.5 = 15/2⁰ past it. We expect that the minute hand will get closer and pass the hour hand and then the angle between them will get larger. We are asked to find the time when the angle within the hands is 64⁰. We just need to set a simple equation and solve for x that is the minimum amount of minutes passing:

After x minutes, the minute hand will move 6x angles; the hour hand will move x/2 angles. The minute hand will move 15/2⁰ initially that is the angle between the hands at 3:15; then it will pass the hour hand by 64⁰. So;

6x = 15/2 + x/2 + 64

 

(11/2)x = 15/2 + 128/2

(11/2)x = 143/2

11x = 143 ® x = 13

After 13 minutes; at 3:28, the angle between hour and minute hands be 64⁰.

 

 

3. C

Let us start analyzing the graph:

Step 1: It shows a quadratic characteristics, the roots of the function are x = – 4 and x = 2. Answer choices B and D are eliminated since they are linear functions.

Step 2: The graph is concave up which means that the term x² has positive coefficient. The vertex passes through (- 1, – 9). The inequality does not cover 0 since the line is dashed.

Point (0, 0) is not included in the inequality. By inserting x = 0 and y = 0, we can check whether A is the answer or C:

x² + 2x – 8 > 0

0² + 2 ^. 0 – 8 > 0

-8 > 0 … this is not a correct statement, so this is not the correct inequality.

x² + 2x – 8 < 0

0² + 2 ^. 0 – 8 < 0

-8 < 0 … this is a correct statement. Yet, it is better that we check the other steps:

Step 1: Find the roots of x² + 2x – 8 = 0:

x² + 2x – 8 = (x + 4)(x – 2) = 0

x = – 4 and x = 2. So, step 1 is proven.

Step 2:

x² + 2x – 8 < 0 … the coefficient of term x² is 1, so the arms of the graph is concave up. The vertex (- 1, – 9) should satisfy x² + 2x – 8 = 0:

(- 1)² + 2(- 1) – 8 = – 9

1 – 2 – 8 = – 9

– 9 = – 9 … The  vertex is correct.

The inequality does not cover 0 since the line is dashed: x² + 2x – 8 < 0. Step 2 is proven.

 

4.  C

Examining the graph, we see that f(- 3) = f(5) = 4; f(10) = 8

f(x) = y ® f^-1(y) = x

So; since f(10) = 8, f^-1(8) = 10

(f(- 3) + f(5) + f(10)) / f^-1(8) = (4 + 4 + 8) / 10 = 1.6

 

 

 

 

 

 

5. D 

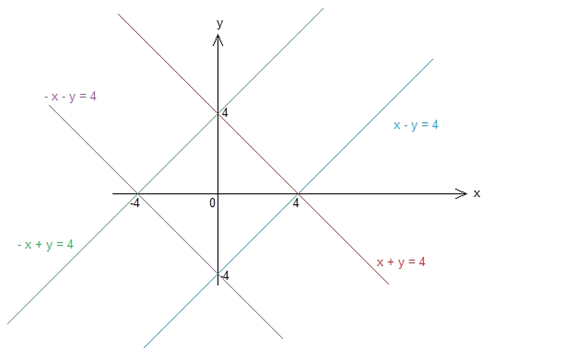
Since this is an absolute value problem, we need to consider negative and positive cases for both x and y:

Let us leave the inequality to the last step and solve |x| + |y| = 4 first:

If x < 0 and y < 0: – x – y = 4

If x < 0 and y > 0: – x + y = 4

If x > 0 and y < 0: x – y = 4

If x > 0 and y > 0: x + y = 4

We obtain four lines. The combination of these four give us the graph of |x| + |y| = 4:

 

Since they are extracted from the same equation; the graph of |x| + |y| = 4 is the rhombus surrounded by

x: [- 4, 4] and y: [- 4, 4].

The function to be drawn the graph of is |x| + |y| £ 4. Checking if origin (0, 0) is within this inequality or not leads us to find the region to be shaded; inside or outside the rhombus:

0 + 0 £ 4 is a correct statement. Therefore, inside region of the rhombus should be shaded.