How to Solve Linear Equations in one variable – Tutorial and Practice Questions
- Posted by Brian Stocker MA
- Date November 27, 2014
- Comments 3 comments
Quick Review and Tutorial – How to Solve Linear Equations in One Variable
Linear equations in one variable x is an equation with the following form:
ax = b
where a and b are some real numbers. If a = 0 and b is different from 0, then the equation has no solution.
Let’s solve one simple example of a linear equation with one variable:
4x – 2 = 2x + 6
When we are given this type of equations, we are always moving variables to the one side of the equation, and real numbers to the other side of the equals sign. Always remember: if you are changing sides, you are changing signs. Let’s move all variables to the left, and real number to the right side:
4x – 2 = 2x + 6
4x – 2x = 6 + 2
2x = 8
x = 8/2
x = 4
When 2x goes to the left it becomes now -2x, and -2 goes to the right and becomes +2. After calculations, we find that x is 4, which is a solution of our linear equation.
Let’s solve a little more complex linear equation:
(2x – 6)/4 + 4 = x
2x – 6 + 16 = 4x
2x – 4x = -16 + 6
-2x = -10
x = -10/-2
x = 5
We multiply whole equation by 4, to lose the fractional line. Now we have a simple linear equation. If we change sides, we change the signs. At the end we do the final calculations.
Linear Equation in One Variable Practice Questions
1. Solve the linear equation:
-x – 7 = -3x – 9
a. -1
b. 0
c. 1
d. 2
2. Solve the linear equation:
3(x + 2) – 2(1 – x) = 4x + 5
a. -1
b. 0
c. 1
d. 2
3. Find the solution for the following linear equation:
5x/2 = (3x + 24)/6
a. -1
b. 0
c. 1
d. 2
4. If a and b are real numbers, solve the following equation:
(a+2)x-b = -2+(a+b)x
a. -1
b. 0
c. 1
d. 2
5. Find the solution for the following linear equation:
1/(4x – 2) = 5/6
a. 0.2
b. 0.4
c. 0.6
d. 0.8
Answer Key
1. A -1
-x – 7 = -3x – 9
-x + 3x = -9 + 7
2x = -2
x = (-2):2
x = -1
2. C 1
3(x + 2) – 2(1 – x) = 4x + 5
3x + 6 – 2 + 2x = 4x + 5
5x + 4 = 4x + 5
5x – 4x = 5 – 4
x = 1
3. D 2
4. A -1
(a + 2)x – b = -2 + (a + b)x
ax + 2x – b = -2 + ax + bx
ax + 2x – ax – bx = -2 + b
2x – bx = -2 + b
(2 – b)x = -(2 – b)
x=-(2-b):(2-b)
x = -1
5. D 0.8
1/(4x – 2) = 5/6 … We can cross multiply:
5(4x – 2) = 1 * 6 … Now, we distribute 5 to the parenthesis:
20x – 10 = 6 … We need x term alone on one side:
20x = 6 + 10
20x = 16 … Dividing both sides by 20:
x = 16/20 … Simplifying by 2 and having 10 in the denominator provides us finding the
decimal equivalent of x:
x = 8/10 = 0.8
Common Mistakes Answering Linear Equation Questions
- Misinterpreting the Question or Setting Up the Equation Incorrectly
- Failing to properly understand what the question is asking.
- Confusing linear equations with other types of algebra.
- Misreading the problem and setting up the wrong equation.
- Basic Arithmetic Errors
- Addition, subtraction, multiplication, or division errors. Basic Math Practice
- Incorrectly applying the order of operations (PEMDAS). Order of Operation Practice
- Solving for the Wrong Variable:
- Solving for the wrong variable.
- Sign Errors:
- Incorrectly using positive and negative signs.
- Failing to change the sign when performing basic operations.
- Fractions and Decimals:
- Incorrectly converting between fractions, decimals, and percentages. Factions, decimals and percent practice
- Incorrect Distribution
- Mistakes when applying the distributive property.
- Forgetting to distribute a negative sign through parentheses.
- Incorrectly Combining Like Terms
- Failing to properly combine like terms.
- Mistaking terms that are not alike for like terms.
- Skipping Steps:
- Skipping steps in the process, leading to errors in the solution.
- Not showing work, making it hard to identify where a mistake was made.
- Checking Solutions:
- Forgetting to plug the solution back into the original equation to check its correctness.
- Assuming an answer is correct without verification.
- Mistakes Graphing
- Errors plotting or connecting points.
- Misinterpreting the slope and intercept in the line equation.
- Time Management:
- Spending too much time on one problem and rushing through others.
- Not allocating enough time to review and check answers. Time Management on a Test
- Anxiety and Pressure:
- Feeling overwhelmed or stressed causing incorrect answers.
- Making careless mistakes due to test anxiety. Test Anxiety Tips
Date Published: Thursday, November 27th, 2014
Date Modified: Tuesday, June 4th, 2024
You may also like

Basic Math Video Tutorials

How to Answer Basic Math Multiple Choice
How to Solve Linear Inequalities – Quick Review and Practice
Basic linear inequalities have one of the following forms: ax + b > 0 ax + b < 0 ax + b > 0 ax + b < 0 where a and b are some real numbers. Our solution to …

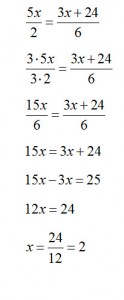
3 Comments
thanks!! found this easy to answer
thanks alot for this preparation
Wow good work