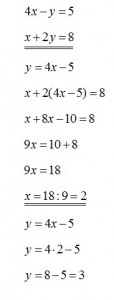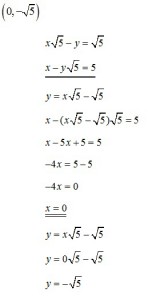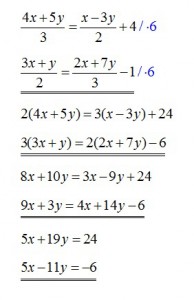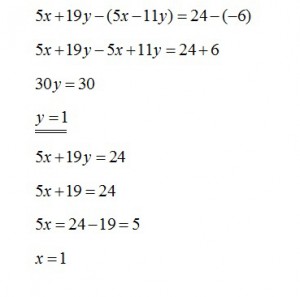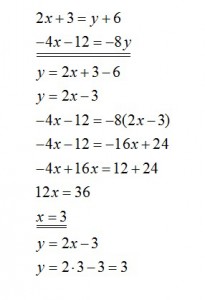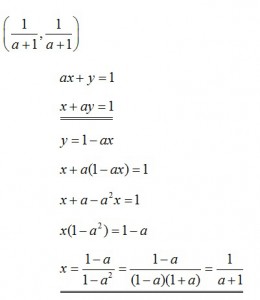How to Solve Linear Equations with 2 Variables – Tutorial and Practice
- Posted by Brian Stocker MA
- Date November 27, 2014
- Comments 0 comment
Linear Equations with 2 Variables
A system of a linear equations have two or more equations and two variables. In a system of linear equations, each equation is a straight line and the solution will be the point where the two lines intersect.
How to Solve Linear Equations with 2 Variables – Quick Review Tutorial
If we have 2 or more linear equations with 2 or more variables, then we have a system of linear equations. Here, we will solve systems with 2 variables, given in 2 linear equations. Idea here is to express one variable using the other variable in one equation, and use it in the second equation, where we would get a linear equation with one variable. Let’s the how it works in one simple example:
x – y = 3
2x + y = 9
y = x – 3
2x + x – 3 = 9
3x = 9 + 3
From the first equation, we express y using x.
In the second equation, we write x – 3 instead of y. And there we get a linear equation with one variable x.
3x = 12
x = 12/3
x = 4
Now that we found x, we can use it to find y.
So, the solution of this system is (x,y) = (4,1)
y = x – 3
y = 4 – 3
y = 1
Let’s solve one more system using a different method:
5x – 3y = 17
x + 3y = 11
Notice that we have -3y in the first equation and +3y in the second. If we add these 2, we get zero, which means we lose variable y. So, we add these 2 equations and we get a linear equation with one variable.
5x – 3y + x + 3y = 17 – 11
6x = 6
x = 1
Now that we have x, we use it to find y.
5 – 3y = 17
-3y = 17 – 5
-3y = 12
y = 12/(-3)
y = -4
Practice Questions
1. Solve the system:
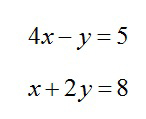
1) (3,2)
2) (3,3)
3) (2,3)
4) (2,2)
2. Solve the system:
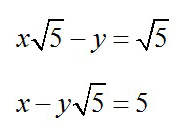
1) (0, -?5)
2) (0, ?5)
3) (-?5, 0)
4) (?5, 0)
3. Find x and y from the following system of equations:
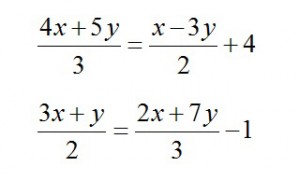
1) (1,3)
2) (2,1)
3) (1,1)
4) (0,1)
4. Find x and y from the following system of equations:
2x+3=y+6
-4x-12=-8y
1) (3,2)
2) (1,3)
3) (3,3)
4) (2,2)
5. Solve the system, if a is some real number:
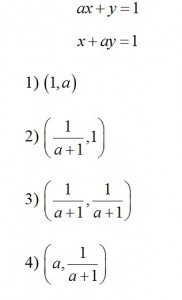
Date Published: Thursday, November 27th, 2014
Date Modified: Monday, June 3rd, 2024
You may also like
Inverse Functions Practice Questions
An inverse function (or anti-function) is a function that “reverses” another function: if the function f applied to an input x, and gives a result of y, then the inverse function g, applied to y, gives the result x, and …
Linear equations in one variable x is an equation with the following form: ax = b where a and b are some real numbers. If a = 0 and b is different from 0, then the equation has no solution. …